Vektor
Veröffentlicht von MSc. Claudia Degrassi in Vektor · Sonntag 18 Feb 2024 · 1:30
Thema: Vektor
Was ist ein Vektor?
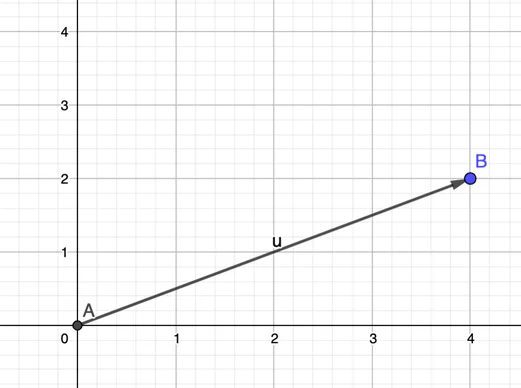
Ein Vektor hat einen Betrag und eine Richtung. Vektoren lassen sich durch Pfeile darstellen, wobei die Spitze des Pfeils die Richtung anzeigt und die Länge des Pfeils den Betrag angibt.
Definition eines Vektors
Ein Vektor besteht aus unendlich vielen parallelen Pfeilen, welche dieselbe Länge und Richtung haben. Allgemein gilt für einen Vektor folgende Schreibweise:
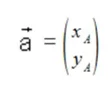
ax und ay sind die Koordinaten (Komponenten ) des Vektors in x- bzw. y-Richtung.
Die Spitze-minus-Schaft-Regel
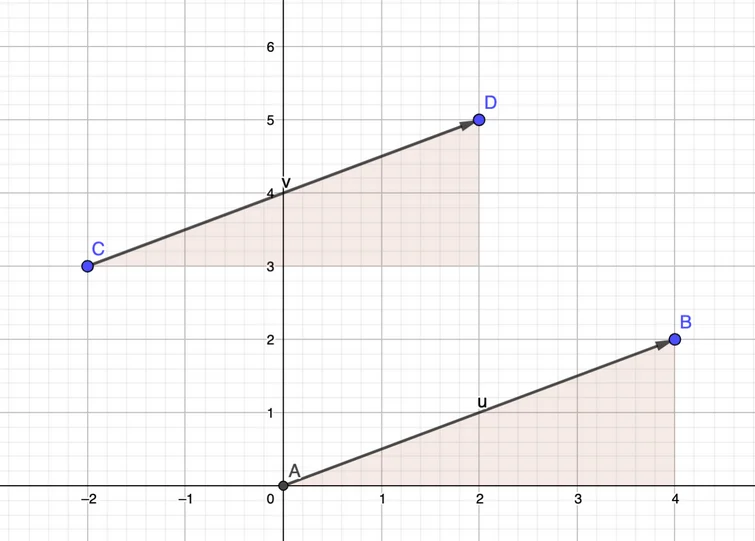
Um einen Vektor zu berechnen, der von beispielsweise A nach B zeigt, also zwischen zwei Punkten liegt, subtrahiert man komponentenweise die Koordinaten des Anfangspunkts (des Schaftes vom Pfeil) vom Endpunkt (der Spitze des Pfeils).

Wann benötige ich den Betrag des Vektors?
Die Länge eines Vektors kann mithilfe des Satzes von Pythagoras berechnet werden.
Daraus ergibt sich folgende Formel:

aus: Mathematik (AHS) Formelsammlung für die standardisierte kompetenzorientierte schriftliche Reifeprüfung (ab Schuljahr 2017/18), Stand: 1. September 2017, Seite 6
Was ist der Unterschied zwischen einem Ortsvektor und einem Punkt?
Der Punkt B hat die Koordinaten B = (4, 2) und liegt an einer bestimmten Stelle. Der Ortsvektor wird als Pfeil eingezeichnet und geht von A nach B.
Die Schreibweise unterscheidet sich ebenfalls, wie in der Abbildung ersichtlich ist.
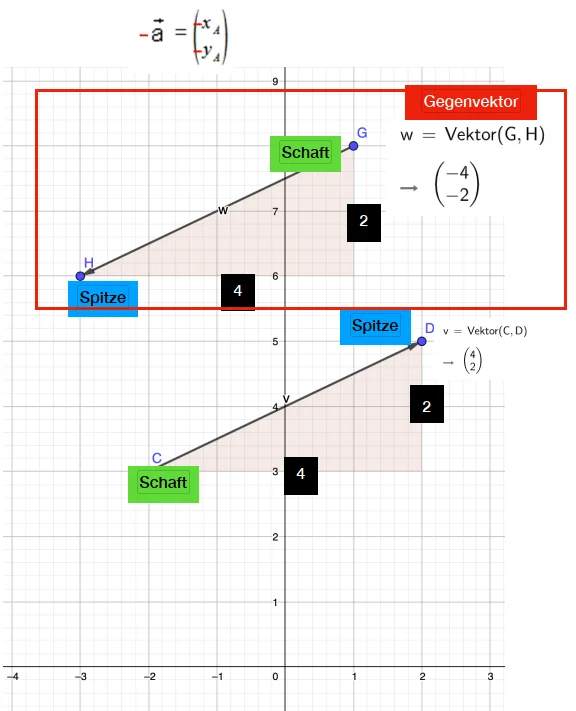
Wann werden Vektoren subtrahiert?
Werden Vektoren subtrahiert, dann bedeutet dies, dass der Vektor mit einem Gegenvektor addiert wird.
Was ist ein Gegenvektor?
Der Gegenvektor wird auch inverser Vektor genannt. Der Gegenvektor hat dabei dieselbe Länge wie der ursprüngliche Vektor, läuft jedoch in die entgegengesetzte Richtung.