Algebra

Veröffentlicht von MSc. Claudia Degrassi in Algebra · Freitag 12 Mai 2023

Thema: Algebra.

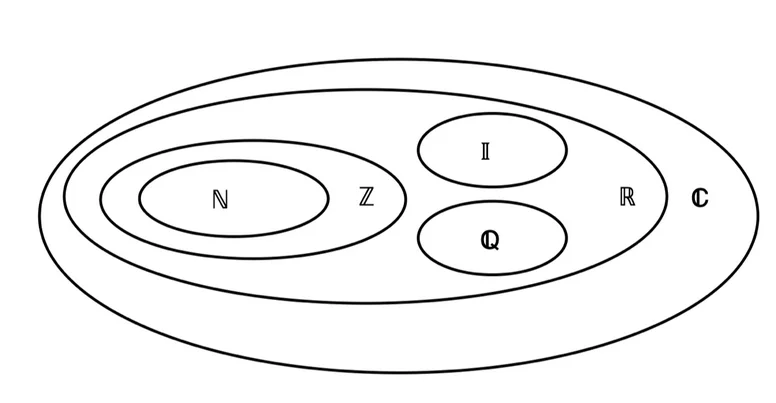
Welche Zahlenmengen gibt es?

• Natürliche Zahlen: ℕ = { 0, 1, 2, 3, 4, … }

Hinweis: Manchmal wird die Null aus der Zahlenmenge der natürlichen Zahlen ausgeschlossen. ℕ* = { 1, 2, 3, 4, … }

• Ganze Zahlen: ℤ = { …, -3, -2, -1, 0, 1, 2, 3, … }

• Rationale Zahlen: ℚ = { -½ ; ⅓ ; 0,666…; 2,25; … }

Hinweis: Rationale Zahlen kann man als Bruch schreiben und sind periodische oder endliche Dezimalzahlen.

• Irrationale Zahlen: 𝕀 = {√2 ; 𝒆 ; π, … }

Hinweis: Irrationale Zahlen sind unendliche nicht periodische Dezimalzahlen.

• Reelle Zahlen: ℝ = ℚ ⋃ 𝕀

Hinweis: Die reellen Zahlen bestehen aus den rationalen Zahlen und den irrationalen Zahlen.

• Komplexe Zahlen: ℂ

Hinweis: Die komplexen Zahlen beinhalten nicht nur alle reellen Zahlen, sondern auch die imaginären Zahlen. z.B.: -i

Venn-Diagramm der Zahlenmengen:

Grundbegriffe:

• Variable: Eine Variable ist eine Unbekannte. Traditionell gesehen verwenden wir in der Mathematik meist Kleinbuchstaben, die als Platzhalter dienen. z.B.: a, b, x, y, …

• Term: Ein Term steht für einen sinnvollen mathematischen Ausdruck, der mit Zahlen, Variablen, Rechenzeichen und Klammern verbunden werden kann. z.B.: 2a + b

• Gleichung: Eine Gleichung ist eine mathematische Aussage. Dabei werden zwei Terme gleichgesetzt.

z.B.: 5 = a ・ b oder 3 = 5x + 2

• Gleichungssystem: Ein Gleichungssystem besteht aus mehreren Gleichungen und Variablen.

• Äquivalenz: Spricht man von einer Äquivalenz, so meint man die Gleichwertigkeit mehrerer mathematischer Aussagen. Werden z.B. beide Seiten einer Gleichung mit derselben Zahl addiert, so sprechen wir in der Mathematik von einer Äquivalenzumformung.

• Grundmenge: Die Grundmenge bestimmt jene Werte und Zahlen, für die eine Variable eingesetzt werden darf!

Wichtig darf! Z.B. darf bei einem Bruch der 1/x lautet für „x“ keine Null eingesetzt werden. Eine Grundmenge muss sinnvoll sein.

• Definitionsmenge: Die Definitionsmenge stellt nun jene Werte dar, die aufgrund von der Bestimmung der Grundmenge als Ergebnis auftreten.

• Lösungsmenge: Die Lösungsmenge enthält jene Zahlen aus der Definitionsmenge, die beim Einsetzen in die Gleichung eine wahre Aussage ergeben.

Verknüpfung von Mengen

Man kann Zahlenmengen miteinander verknüpfen. Daraus ergeben sich neue Mengen:

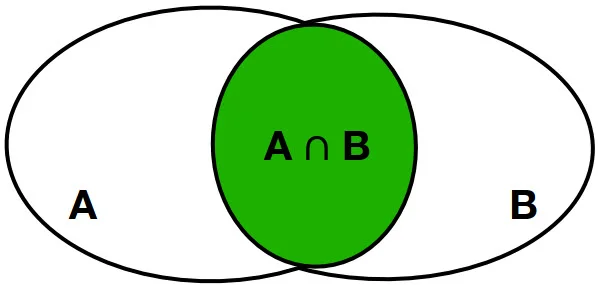
Durchschnittsmenge = gesprochen „A geschnitten B“ = A ∩ B

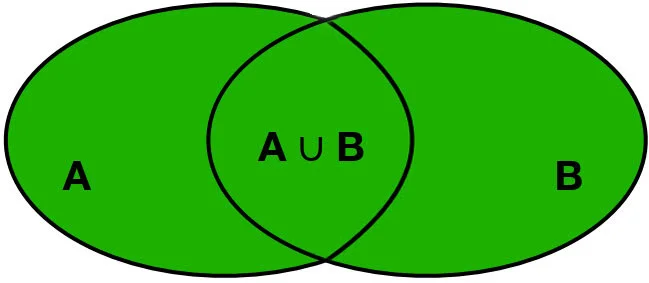
Vereinigungsmenge = gesprochen „A vereinigt B“ = A ∪ B

Diﬀerenzmenge = gesprochen „A ohne B“ = A ∖ B

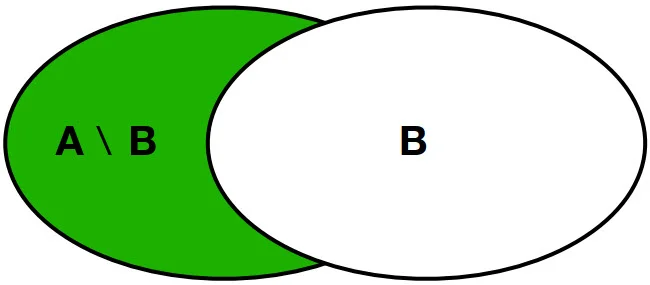
Komplementärmenge = A’ = wenn A ein Teil einer Grundmenge G ist

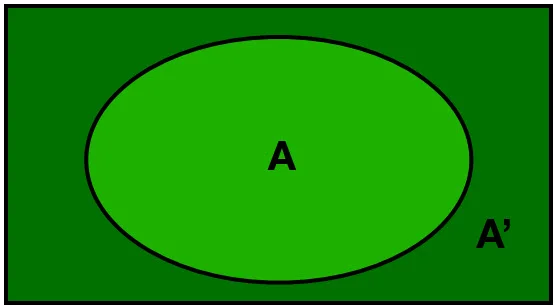
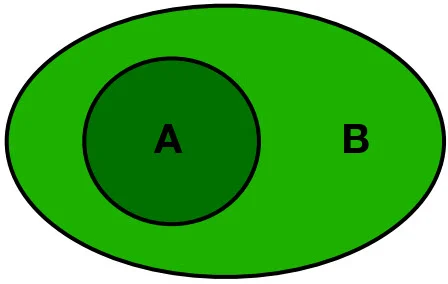
Teilmenge = alle Elemente von A sind auch Elemente von B = A ⊆ B